努力打造河南专升本万人院校！
24小时咨询热线：4006868751
随学(文都)专升本2016年高数真题
一．选择题（每小题2分，共60分）
1.函数
的定义域是（ ）
A.(
,-1］ B. (,-1) C. (,1］ D. (,1)
2.函数
是（ ）
A．奇函数 B.偶函数 C.非奇非偶函数 D。无法判断奇偶性
3．已知
，则
（ ）
A.
B.
C.
D.
4.下列极限不存在的是（ ）
A.
B.
C.
D.
5.极限
的值是（ ）
A.0 B.1 C.-1 D.-2
6.已知极限
，则a的值是（ ）
A.1 B.-1 C.2 D.
7.已知当x
0时，
,则a的值是（ ）
A.1 B.2 C. D.-1
8.已知函数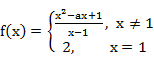
则在点x=1处，下列结论正确的是（ ）
A.
时，
必连续 B.时，不连续
C.
时，连续 D.
时，必连续
9.已知函数
在点
处可导，函数
,则
（ ）
A.
B.
C.
D.
10.函数
在点
处（ ）
A.不连续 B.连续且可导 C.既不连续也不可导 D.连续但不可导
11.若曲线
与曲线
在自变量
时的切线相互垂直，则
应为（ ）
A.
B.
C.
D.
12.已知
在闭区间
上满足罗尔中值定理，则在开区间
内使
成立的
（ ）
A.0 B.1 C.
D.2
13.设函数
在区间内连续，若
时，
；
时，
，则在区间内（ ）
A.
是函数的极小值 B.是函数的极大值
C.不是函数的极值 D.不一定是函数的极值
14.设函数
在区间
内具有二阶导数，若时，
；
时，
，则（ ）
A.
是函数的极大值
B.点
是曲线的拐点
C.是函数的极小值
D. 点不是曲线的拐点
15.已知曲线
,则（ ）
A.在
内单调递减且形状为凸
B.在内单调递增且形状为凹
C.在
内单调递减且形状为凸
D.在内单调递增且形状为凹
16.已知
是的一个原函数，则不定积分
（ ）
A.
B.
C.
D.
17.设函数
,则
（ ）
A.
B.
C.
D.
18.定积分
（ ）
A.
B.
C.0 D.2a
19.由曲线
与直线,,
所围成的平面图形的面积是（ ）
A.
B.1 C.
D.
20.设定积分
,
,则（ ）
A.
B.
C.
D.不能确定
与
的大小
21.向量
的方向角是（ ）
A.
,
, 
B.
,
,
C.,, D.
,,
22.已知
是微分方程
的一个解。则常数a=（ ）
A.1 B. C.3 D.
23.下列微分方程可进行变量分离的是（ ）
A.
B.
C.
D.
24.设二元函数
,则
（ ）
A.
B.
C.2y D.2x
25.用钢板做成一个表面积为
的有盖长方体水箱，欲使水箱的容积最大，则水箱的最大容积为（ ）
A.
B.
C.
D.
26.设
,则二重积分
（ ）
A.16
B.8 C.4 D.3
27.已
,则交换积分顺序后
（ ）
A.
B.
C.
D.
28.设L为连接点
与点
的直线段，则曲线积分
（ ）
A.1 B.2 C.3 D.
29.下列级数发散的是（ ）
A.
B.
C.
D.
30.已知级数
,则下列结论正确的是（ ）
A.若
,则收敛
B.若部分和数列
有界，则收敛
C.
收敛，则
D.
收敛，则
收敛
二、填空题（每小题2分，共20分）
31.函数
的反函数是
__________
32.极限
___________
33.已知函数
，则点是的__________间断点.
34.函数
在点
处的近似值为__________.
35.不定积分
____________.
36.定积分
=_____________.
37.函数
在点
处的全微分
_____________.
同平行的单位向量是______________.
39.微分方程
的通解是____________.
40.幂级数
的收敛半径为_____________.
三、计算题（每小题5分，共50分）
41.计算极限
42.求函数
的导函数.
43.计算不定积分
.
44.计算定积分
.
45.设直线L:
,求过点A(0,1,2)且平行于直线L的直线方程.
46.已知函数
方程
所确定，求全微分
.
47.已知
,计算二重积分
’
48.求微分方程
的通解.
49.求幂级数
的收敛区间.
50.求级数
的和函数.
51.求由直线,
,及曲线
所围成平面图形的面积.
52.某工厂生产计算器，若日产量为
台的成本函数为
,收入函数为
,且产销平衡，试确定日生产多少台计算器时，工厂的利润最大?
五、证明题（6分）
53.已知方程
有一负根
,证明方程
必有一个大于
的负根.
